Page 58 - 《华中农业大学学报（社会科学版）》2020年第4期

第 ４ 期 杨 鑫 等: 农业技术采用、 时间重配置与农户收入 ５ ３

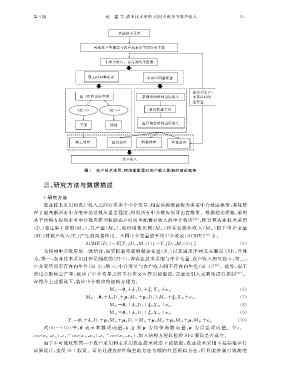
图 １ 农户技术采用、 时间重配置对农户收入影响的理论框架

三、 研究方法与数据描述

１． 研究方法
农业技术采用和农户收入之间存在多个中介变量, 相应的模型就称为多重中介效应模型, 其优势
在于能判断所有中介变量的总效应显著程度, 得到所有中介效应的可比性数值.根据理论框架, 采用
基于结构方程的多重中介效应模型检验农户时间重配置对收入的中介效应 [ ２４ ] , 即计算农业技术采用

)
)
) )、 溢价销售比例( M３i 和非农就业收入( M４i 四个中介变量
( D i 通过雇工费用( M１i )、 总产量( M２i
[ ２５ ]
)
)
( Mi 对农户收入( Y i 产生的间接作用.不同中介变量的平均中介效应( ACME ) 为:
{
{
, ()
)
ACME ( D i ＝E [ Y i D i Mi １ } －Y i D i Mi ０ } ] ( ５ )
, ()
为得到中介效应的一致估计, 需要控制可观测混杂变量( X i 以及满足序列无关假设 ( SI ), 具体
)
为: 第一, 农业技术采用过程是随机的( SIＧ１ ), 即农业技术采用与中介变量、 农户收入相互独立; 第二,
中介变量间不存在内生性( SIＧ２ ); 第三, 中介变量与农户收入间不存在内生性( SIＧ３ ) .此外, 雇工
[ ２６ ]
费用会影响总产量, 破坏了中介变量之间不存在交互作用的假设, 需通过引入交乘项进行控制 [ ２７ ] .
在符合上述假设下, 估计中介效应的结构方程为:
( ６ )
M１i＝θ １＋λ １ D i＋ ξ １X１i＋κ １i
( ７ )
M２i＝θ ２＋λ ２ D i＋ μ １M１i＋ μ ２ D i×M１i＋ ξ ２X２i＋κ ２i
( ８ )
M３i＝θ ３＋λ ３ D i＋ ξ ３X３i＋κ ３i
( ９ )
M４i＝θ ４＋λ ４ D i＋ ξ ４X４i＋κ ４i
( １０ )
Y i＝θ ５＋λ ５ D i＋ μ ３M１i＋ μ ４ D i×M１i＋ μ ５M２i＋ μ ６M３i＋ μ ７M４i＋κ ５i
式( ６ ) ~ ( １０ ) 中, θ 表 示 常 数 项 向 量, λ 、 和 μ 为 待 估 参 数 向 量, κ 为 误 差 项 向 量. 令 e １ ＝
ξ
, ), , ), , ), 加入结构方程以检验 SIＧ２ 假设是否成立.
cov ( κ ２i κ ３i e ２＝cov ( κ ３i κ ４i e ３＝cov ( κ ２i κ ４i
由于不可能收集同一个农户采用和未采用农业技术状态下的数据, 农业技术采用不是标准平行
试验设计, 违反 SIＧ１ 假设.常见处理选择性偏差的方法为倾向性匹配得分法, 但只能控制可观测变